@TOC
一、线性回归
1.基本概念
线性回归是回归问题中的一种,线性回归假设目标值与特征之间线性相关,即满足一个多元一次方程。通过构建损失函数,来求解损失函数最小时的参数w和b。通长我们可以表达成如下公式:
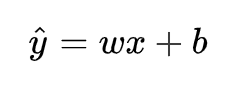
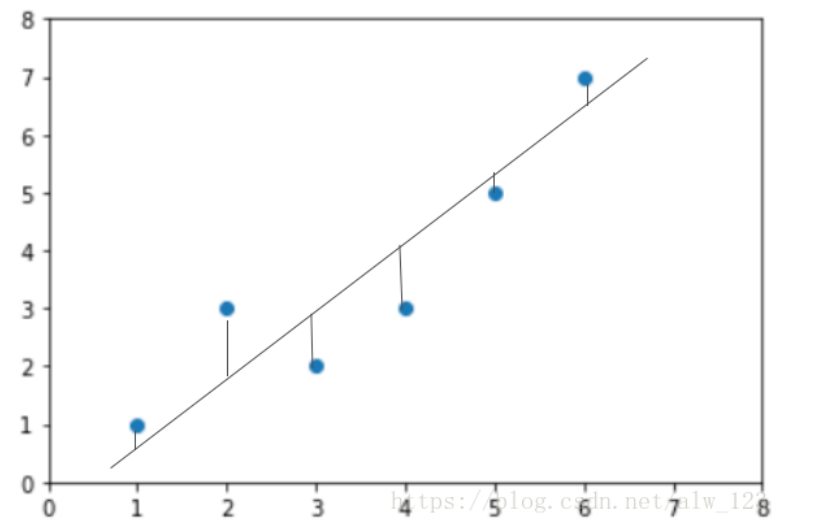
y^为预测值,自变量x和因变量y是已知的,而我们想实现的是预测新增一个x,其对应的y是多少。因此,为了构建这个函数关系,目标是通过已知数据点,求解线性模型中w和b两个参数。 我的理解,线性回归无非就是在N维空间中根据欧氏距离加和来量化预测结果和真实结果的误差找一个形式最像直线方程一样的函数来拟合数据。
2.代码实现
实现代码如下:
from numpy import *
import matplotlib.pyplot as plt
#读取数据
def loadDataSet(filename):
numFeat = len(open(filename).readline().split('\t'))-1
dataMat = []; labelMat = []
fr = open(filename)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat, labelMat
#标准线性回归函数
def standRegres(xArr, yArr):
xMat = mat(xArr)
yMat = mat(yArr).T
xTx = xMat.T * xMat
#判断行列式为零,则无法求逆
if linalg.det(xTx) == 0:
print('the matrix is singular, cannot do inverse')
return
ws = (xTx).I * (xMat.T*yMat)
return ws
#拟合数据
xArr, yArr = loadDataSet('ex0.txt')
ws = standRegres(xArr, yArr)
xMat = mat(xArr)
yMat = mat(yArr)
yHat = xMat*ws
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xMat[:,1].flatten().A[0], yMat.T[:,0].flatten().A[0])
xCopy = xMat.copy()
xCopy.sort(0)
yHat = xCopy*ws
ax.plot(xCopy[:,1], yHat)
plt.show()
二、逻辑回归
1.基本概念
使用线性回归来处理 0/1 分类问题比较困难,因此引入逻辑回归来完成 0/1 分类问题,逻辑一词也代表了是(1)和非(0)。
Sigmoid预测函数
在逻辑回归中,定义预测函数为:
 g(z) 称之为 Sigmoid Function,亦称 Logic Function
g(z) 称之为 Sigmoid Function,亦称 Logic Function
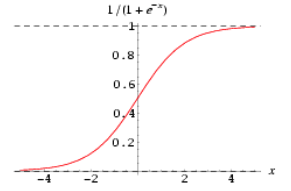
我的理解:逻辑回归就是输入不定,但是输出只有0/1,决定输入与输出之间变化的便是决策边界。
2.代码实现
代码如下(示例):
from numpy import *
filename='...\\testSet.txt' #文件目录
def loadDataSet(): #读取数据(这里只有两个特征)
dataMat = []
labelMat = []
fr = open(filename)
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #前面的1,表示方程的常量。比如两个特征X1,X2,共需要三个参数,W1+W2*X1+W3*X2
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
def sigmoid(inX): #sigmoid函数
return 1.0/(1+exp(-inX))
def gradAscent(dataMat, labelMat): #梯度上升求最优参数
dataMatrix=mat(dataMat) #将读取的数据转换为矩阵
classLabels=mat(labelMat).transpose() #将读取的数据转换为矩阵
m,n = shape(dataMatrix)
alpha = 0.001 #设置梯度的阀值,该值越大梯度上升幅度越大
maxCycles = 500 #设置迭代的次数,一般看实际数据进行设定,有些可能200次就够了
weights = ones((n,1)) #设置初始的参数,并都赋默认值为1。注意这里权重以矩阵形式表示三个参数。
for k in range(maxCycles):
h = sigmoid(dataMatrix*weights)
error = (classLabels - h) #求导后差值
weights = weights + alpha * dataMatrix.transpose()* error #迭代更新权重
return weights
def stocGradAscent0(dataMat, labelMat): #随机梯度上升,当数据量比较大时,每次迭代都选择全量数据进行计算,计算量会非常大。所以采用每次迭代中一次只选择其中的一行数据进行更新权重。
dataMatrix=mat(dataMat)
classLabels=labelMat
m,n=shape(dataMatrix)
alpha=0.01
maxCycles = 500
weights=ones((n,1))
for k in range(maxCycles):
for i in range(m): #遍历计算每一行
h = sigmoid(sum(dataMatrix[i] * weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i].transpose()
return weights
def stocGradAscent1(dataMat, labelMat): #改进版随机梯度上升,在每次迭代中随机选择样本来更新权重,并且随迭代次数增加,权重变化越小。
dataMatrix=mat(dataMat)
classLabels=labelMat
m,n=shape(dataMatrix)
weights=ones((n,1))
maxCycles=500
for j in range(maxCycles): #迭代
dataIndex=[i for i in range(m)]
for i in range(m): #随机遍历每一行
alpha=4/(1+j+i)+0.0001 #随迭代次数增加,权重变化越小。
randIndex=int(random.uniform(0,len(dataIndex))) #随机抽样
h=sigmoid(sum(dataMatrix[randIndex]*weights))
error=classLabels[randIndex]-h
weights=weights+alpha*error*dataMatrix[randIndex].transpose()
del(dataIndex[randIndex]) #去除已经抽取的样本
return weights
def plotBestFit(weights): #画出最终分类的图
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i])== 1:
xcord1.append(dataArr[i,1])
ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1])
ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
def main():
dataMat, labelMat = loadDataSet()
weights=gradAscent(dataMat, labelMat).getA()
plotBestFit(weights)
if __name__=='__main__':
main()
参考资料 https://zhuanlan.zhihu.com/p/74874291 https://www.cnblogs.com/geo-will/p/10306691.html
三 决策树
1.基本概念
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。在机器学习中,决策树是一个预测模型,他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。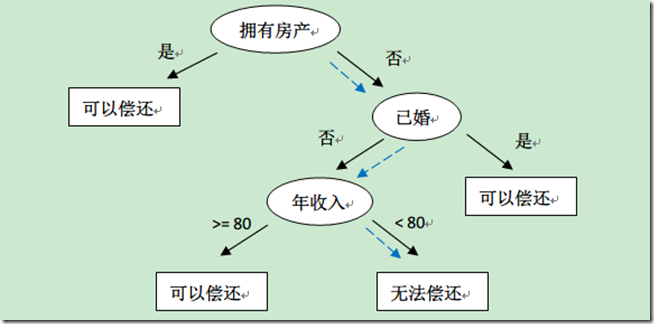
2.代码实现
from math import log
import operator
def calcShannonEnt(dataSet): # 计算数据的熵(entropy)
numEntries=len(dataSet) # 数据条数
labelCounts={}
for featVec in dataSet:
currentLabel=featVec[-1] # 每行数据的最后一个字(类别)
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1 # 统计有多少个类以及每个类的数量
shannonEnt=0
for key in labelCounts:
prob=float(labelCounts[key])/numEntries # 计算单个类的熵值
shannonEnt-=prob*log(prob,2) # 累加每个类的熵值
return shannonEnt
def createDataSet1(): # 创造示例数据
dataSet = [['长', '粗', '男'],
['短', '粗', '男'],
['短', '粗', '男'],
['长', '细', '女'],
['短', '细', '女'],
['短', '粗', '女'],
['长', '粗', '女'],
['长', '粗', '女']]
labels = ['头发','声音'] #两个特征
return dataSet,labels
def splitDataSet(dataSet,axis,value): # 按某个特征分类后的数据
retDataSet=[]
for featVec in dataSet:
if featVec[axis]==value:
reducedFeatVec =featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
def chooseBestFeatureToSplit(dataSet): # 选择最优的分类特征
numFeatures = len(dataSet[0])-1
baseEntropy = calcShannonEnt(dataSet) # 原始的熵
bestInfoGain = 0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value)
prob =len(subDataSet)/float(len(dataSet))
newEntropy +=prob*calcShannonEnt(subDataSet) # 按特征分类后的熵
infoGain = baseEntropy - newEntropy # 原始熵与按特征分类后的熵的差值
if (infoGain>bestInfoGain): # 若按某特征划分后,熵值减少的最大,则次特征为最优分类特征
bestInfoGain=infoGain
bestFeature = i
return bestFeature
def majorityCnt(classList): #按分类后类别数量排序,比如:最后分类为2男1女,则判定为男;
classCount={}
for vote in classList:
if vote not in classCount.keys():
classCount[vote]=0
classCount[vote]+=1
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
def createTree(dataSet,labels):
classList=[example[-1] for example in dataSet] # 类别:男或女
if classList.count(classList[0])==len(classList):
return classList[0]
if len(dataSet[0])==1:
return majorityCnt(classList)
bestFeat=chooseBestFeatureToSplit(dataSet) #选择最优特征
bestFeatLabel=labels[bestFeat]
myTree={bestFeatLabel:{}} #分类结果以字典形式保存
del(labels[bestFeat])
featValues=[example[bestFeat] for example in dataSet]
uniqueVals=set(featValues)
for value in uniqueVals:
subLabels=labels[:]
myTree[bestFeatLabel][value]=createTree(splitDataSet\
(dataSet,bestFeat,value),subLabels)
return myTree
if __name__=='__main__':
dataSet, labels=createDataSet1() # 创造示列数据
print(createTree(dataSet, labels)) # 输出决策树模型结果
四 支持向量机(SVM)
1.基本概念
支持向量机(Support Vector Machine, SVM)是一类按监督学习(supervised learning)方式对数据进行二元分类的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面(maximum-margin hyperplane) 。SVM使用铰链损失函数(hinge loss)计算经验风险(empirical risk)并在求解系统中加入了正则化项以优化结构风险(structural risk),是一个具有稀疏性和稳健性的分类器 = 。SVM可以通过核方法(kernel method)进行非线性分类,是常见的核学习(kernel learning)方法之一 。
应用在人像识别、文本分类等模式识别(pattern recognition)
2.代码实现
#SVM分类器的编写
class SVM:
def __init__(self, max_iter=100, kernel='linear'):
self.max_iter = max_iter
self._kernel = kernel
def init_args(self, features, labels):
self.m, self.n = features.shape
self.X = features
self.Y = labels
self.b = 0.0
# 将Ei保存在一个列表里
self.alpha = np.ones(self.m)
self.E = [self._E(i) for i in range(self.m)]
# 松弛变量
self.C = 1.0
def _KKT(self, i):
y_g = self._g(i)*self.Y[i]
if self.alpha[i] == 0:
return y_g >= 1
elif 0 < self.alpha[i] < self.C:
return y_g == 1
else:
return y_g <= 1
# g(x)预测值,输入xi(X[i])
def _g(self, i):
r = self.b
for j in range(self.m):
r += self.alpha[j]*self.Y[j]*self.kernel(self.X[i], self.X[j])
return r
# 核函数
def kernel(self, x1, x2):
if self._kernel == 'linear':
return sum([x1[k]*x2[k] for k in range(self.n)])
elif self._kernel == 'poly':
return (sum([x1[k]*x2[k] for k in range(self.n)]) + 1)**2
return 0
# E(x)为g(x)对输入x的预测值和y的差
def _E(self, i):
return self._g(i) - self.Y[i]
def _init_alpha(self):
# 外层循环首先遍历所有满足0<a<C的样本点,检验是否满足KKT
index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
# 否则遍历整个训练集
non_satisfy_list = [i for i in range(self.m) if i not in index_list]
index_list.extend(non_satisfy_list)
for i in index_list:
if self._KKT(i):
continue
E1 = self.E[i]
# 如果E2是+,选择最小的;如果E2是负的,选择最大的
if E1 >= 0:
j = min(range(self.m), key=lambda x: self.E[x])
else:
j = max(range(self.m), key=lambda x: self.E[x])
return i, j
def _compare(self, _alpha, L, H):
if _alpha > H:
return H
elif _alpha < L:
return L
else:
return _alpha
def fit(self, features, labels):
self.init_args(features, labels)
for t in range(self.max_iter):
# train
i1, i2 = self._init_alpha()
# 边界
if self.Y[i1] == self.Y[i2]:
L = max(0, self.alpha[i1]+self.alpha[i2]-self.C)
H = min(self.C, self.alpha[i1]+self.alpha[i2])
else:
L = max(0, self.alpha[i2]-self.alpha[i1])
H = min(self.C, self.C+self.alpha[i2]-self.alpha[i1])
E1 = self.E[i1]
E2 = self.E[i2]
# eta=K11+K22-2K12
eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2], self.X[i2]) - 2*self.kernel(self.X[i1], self.X[i2])
if eta <= 0:
# print('eta <= 0')
continue
alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E1 - E2) / eta#此处有修改,根据书上应该是E1 - E2,书上130-131页
alpha2_new = self._compare(alpha2_new_unc, L, H)
alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)
b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i1]) * (alpha2_new-self.alpha[i2])+ self.b
b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i2]) * (alpha2_new-self.alpha[i2])+ self.b
if 0 < alpha1_new < self.C:
b_new = b1_new
elif 0 < alpha2_new < self.C:
b_new = b2_new
else:
# 选择中点
b_new = (b1_new + b2_new) / 2
# 更新参数
self.alpha[i1] = alpha1_new
self.alpha[i2] = alpha2_new
self.b = b_new
self.E[i1] = self._E(i1)
self.E[i2] = self._E(i2)
return 'train done!'
def predict(self, data):
r = self.b
for i in range(self.m):
r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
return 1 if r > 0 else -1
def score(self, X_test, y_test):
right_count = 0
for i in range(len(X_test)):
result = self.predict(X_test[i])
if result == y_test[i]:
right_count += 1
return right_count / len(X_test)
def _weight(self):
# linear model
yx = self.Y.reshape(-1, 1)*self.X
self.w = np.dot(yx.T, self.alpha)
return self.w
五 全连接神经网络DNN
1.基本概念
多层感知器组成的层式结构,每个感知器(神经元)与所有输入均有权重连接的网络,叫做全连接网络。
一般神经网络包括输入层、隐藏层和输出层,一个DNN结构只有一个输入层,一个输出层,输入层和输出层之间的都是隐藏层。每一层神经网络有若干神经元(下图中蓝色圆圈),层与层之间神经元相互连接,层内神经元互不连接,而且下一层神经元连接上一层所有的神经元。
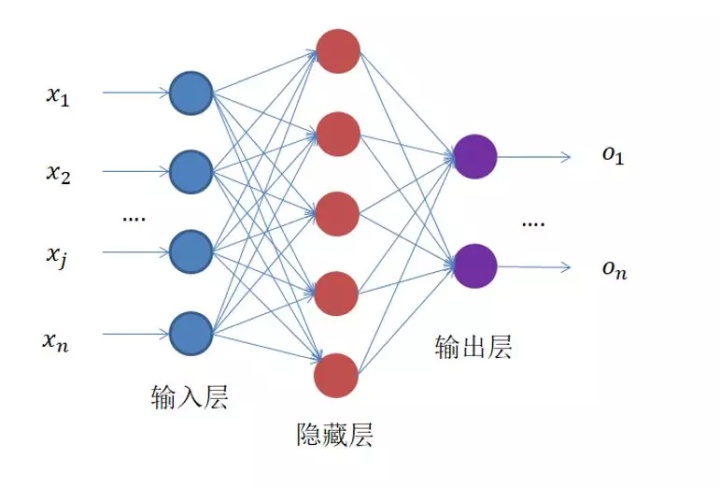
全连接神经网络前向传播
假设我们输入的矩阵维度为6*1,中间隐层数的神经元个数为
全连接神经网络反向传播
2.代码实现
class Network():
def __init__(self, params_array, activator):
#params_array为层维度信息超参数数组
#layers为网络的层集合
self.layers = []
for i in range(len(params_array) - 1):
self.layers.append(FullConnectedLayer(params_array[i], params_array[i+1], activator))
#网络前向迭代
def predict(self, sample):
#下面一行的output可以理解为输入层输出
output = sample
for layer in self.layers:
layer.forward(output)
output = layer.output_data
return output
#网络反向迭代
def calc_gradient(self, label):
delta = (self.layers[-1].output_data - label)
for layer in self.layers[::-1]:
delta = layer.backward(delta)
return delta
#一次训练一个样本 ,然后更新权值
def train_one_sample(self, sample, label, lr):
self.predict(sample)
Loss = self.loss(self.layers[-1].output_data, label)
self.calc_gradient(label)
self.update(lr)
return Loss
#一次训练一批样本 ,然后更新权值
def train_batch_sample(self, sample_set, label_set, lr, batch):
Loss = 0.0
for i in range(batch):
self.predict(sample_set[i])
Loss += self. loss(self.layers[-1].output, label_set[i])
self.calc_gradient(label_set[i])
self.update(lr, 1)
return Loss
def update(self, lr, MBGD_mode = 0):
for layer in self.layers:
layer.update(lr, MBGD_mode)
def loss(self, pred, label):
return 0.5 * ((pred - label) * (pred - label)) .sum()
def gradient_check(self, sample, label):
self.predict(sample)
self.calc_gradient(label)
incre = 10e-4
for layer in self.layers:
for i in range(layer.w.shape[0]):
for j in range(layer.w.shape[1]):
layer.w[i][j] += incre
pred = self.predict(sample)
err1 = self.loss(pred, label)
layer.w[i][j] -= 2 * incre
pred = self.predict(sample)
err2 = self.loss(pred, label)
layer.w[i][j] += incre
pred_grad = (err1 - err2) / (2 * incre)
calc_grad = layer.w_grad[i][j]
print 'weights(%d,%d): expected - actural %.4e - %.4e' % (
i, j, pred_grad, calc_grad)
知识补充
损失函数
损失函数:损失函数用来评价模型的预测值和真实值不一样的程度,损失函数越好,通常模型的性能越好。不同的模型用的损失函数一般也不一样。
回归分析
回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析,时间序列模型以及发现变量之间的因果关系。通常使用曲线/线来拟合数据点,目标是使曲线到数据点的距离差异最小。
总结
本篇讲解了常见机器学习算法,进行了代码的实现。常规使用的时候并不用在意其模型实现,只需要选择合适的模型,然后选择合适的参数。模型没有最好的,模型只有最合适的。